Mutual Autism in Random Walks
Thiago RS Moura*, Anderson JA Ramos and Andŕe JA Ramos
DOI10.4172/2472-1786.100067
Thiago RS Moura1*, Anderson JA Ramos1 and Andre JA Ramos2
1Faculty of Sciences, Federal University of Pará, Salinópolis - PA, 68721-000, Brazil
2Faculty of Computer Science, Federal University of Pará, Belém - PA, 66075- 110, Brazil
- *Corresponding Author:
- Thiago RS Moura
Faculty of Sciences
Federal University of Pará
Interdisciplinary Innovation Laboratory
Raimundo Santana Street, Salinópolis - PA, 68721-000, Brazil
E-mail: trsmoura@yahoo.com.br
Received Date: January 26, 2018; Accepted Date: March 02, 2018; Published Date: March 09, 2018
Citation: Moura TRS, Ramos AJA, Ramos AJA (2018) Mutual Autism in Random Walks. J Child Dev Disord. 4:4. doi: 10.4172/2472-1786.100067
Abstract
Children with autism spectrum disorder have deficits in their communication and social interaction. Symptoms such as lack of socio-emotional reciprocity, problems to initiate or respond to social interactions, understand, develop relationships, abnormalities in eye contact and body expression, exhibit restricted interests, and thus patterns of repetitive behavior are observed in routine neurological exams. Based on these symptoms and new diagnostic tools, which assess social communication and interaction in multiple contexts, we propose discrete random walks as a diagnostic tool. Our model, based on symptoms of autism such as lack of social interaction and restricted interests, consists of random walks that can learn and imitate each other microscopically with probability f (1 − f, otherwise). In this perspective, the probability f quantifies the mutual interaction between pairs of random walkers, While the exponent of Hurst (H) classifies the difusivos regimes, and their variation quantifies the transitions between varying degrees of autism to the pair of random walkers. We report how the interaction of an individual who presents (does not present) the symptoms of autism, affects the diffusive regimes of an individual who does not have this disorder.
Keywords
Autism; Non-Markovian processes; Anomalous diffusion; Diagnosis tools
Introduction
Development disorders are classified in as specific and pervasive. The specific disorder is characterized by developmental delays in a specific area or specific areas, while the pervasive disorder presents deficiencies in basic functions, in multiple contexts that include socialization and communication. Pervasive developmental disorders (PDDs) are part of the group of disorders of the autistic spectrum, known as neurodevelopmental disorder. The PDDs is a psychiatric condition caused by brain damage, not degenerative, accompanied by symptoms such as: delay in verbal and non-verbal communication; resistance to routine change; restricted and persistent interests in relation to an activity, topic, object, speech, idiosyncratic phrases, and so on; abnormalities in eye contact and body expression; difficulties in initiating and maintaining social relations. Each of these symptoms can be classified as mild, moderate or severe. These and other symptoms are part of the diagnostic criteria for autism spectrum disorders, more details can be found in [1].
Motivated by the possibility of developing new diagnostic tools, based on the symptoms and diagnostic criteria of autism, we seek to introduce discrete random walks as a diagnostic tool for autism. The literature provides examples on applications of random walks in biological systems and for medical purposes in [2-4].
The model Schütz and Trimper, also known as Elephant Random Walk (ERW), is a particular model of random walking which has characteristics that are appropriate for the construction of our model. Among them we highlight: random walker has the memory of each of his/her decisions taken throughout his/ her history, i.e., every decision is stored in memory at every instant of time, and this particular characteristic attributes a non-Markovian behavior in random walk; the model presents an accurate analytical solution; their diffusive regimes are well known and is considered the ideal model as it is the limit of best memory for discrete random walks. The ERW has been used as the basis for the construction of several other theoretical models, which display and enrich the spectrum of diffusive regimes and new search engines in memory, among other characteristics [5]. Some of these models, inspired by the Schütz and Trimper model, are: random Alzheimer’s walks, which deal with memory loss leading to the appearance of super-diffusion [6-10]; the model of random walks with Gaussian memory profile, having a connection with the model of Alzheimer’s walks when the gaussian width has a specific magnitude; the exponential model, which solves the apparent paradox, of a stochastic process with exponential distribution, cannot lead to super-diffusion [11]; the random walks with q-exponential memory profile, which present a super diffusive transient when the time is arbitrarily large [12], and finally, we highlight the model with binomial memory profile, which presents narrow log-periodic modulations [13].
For our problem, we define the ERW model with the pattern that presents diffusive regimes, quantified by the Hurst exponent (H), which represents an individual who does not present PDDs symptoms. Therefore, we describe appropriately the majority characteristics of the ERW model that are present in the random walks models described above and which are also present in our model [6-13].
Nevertheless, we describe the relevant aspects of the model of Schütz and Trimper and its main characteristics, in addition to the dissemination regimes. The model of random walks with Gaussian memory profile, having a connection with the model of Alzheimer’s walks, taken at every moment of time, depends on the spectrum of decisions taken in every previous history of the walker in an equiprobable manner. To reclaim each past decision in an equiprobable way is to be responsible for shaping a random walk with a uniform memory profile. Given this, the probability of an action taken in the past to be remembered is 1/t, where t is the current time. The random walk is recorded at all times and this aspect attributes to the process a non-Markovian characteristic.
The stochastic dynamics of the process occur in the following way: the walker starts in time t0 and in a position x0. At every instant of time, the walker walks one step to the right or one step to the left, with probability p and 1 − p, respectively. For this process, the stochastic evolution equation is given by
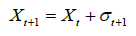 (1)
(1)
for the time t + 1. At every instant of time, the walker walks one step to the right or one step to the left, with probability p and 1 − p, respectively. Memory consists of a set of random variables σÃâ¦ÃÂ¥ for the time Ãâ¦ÃÂ¥ < t that the walker can recover. This process occurs as follows:
(a) in time t + 1, a number Ãâ¦ÃÂ¥ of the set {1, 2, ..., t} is chosen randomly with uniform probability 1/t;
(b) the variable σ is determined stochastically by following the following relationships, σt+1 = σt, with probability p and with probability 1 − p.
The first step in the instant t=1, occurs according to the following dynamics: the walker is in position X0 and moves to the right with probability q or to the left with probability 1 − q, i.e.,σ1=+1 with probability q and σ1=−1 with probability 1 − q the stochastic evolution equation is
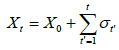 (2)
(2)
The parameter p is the probability of the walker repeating an action from the past at a time Ãâ¦ÃÂ¥. When p>1/2 the walker presents a persistent behavior, this is characterized by the repetition of past actions. For p<1/2, the walker takes an action contrary to the action that was selected, presenting an anti-persistent behavior. For the value of p=1/2 the random walk is Markovian. In the boundary regions of p=0 and p=1, two extreme behaviors arise. In p=0 the maximum of the persistent behavior occurs, while in p=1, the maximum of the persistent behavior occurs. In the latter case, the movement is ballistic, characterized by the typical value of the Hurst exponent (H=1) [5].
The first moment of the position is given by
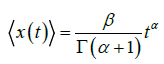 (3)
(3)
and β=2q − 1, α=2p − 1 and Γ is the gamma function. The parameters α and β are defined in the interval [ -1, 1]. Using the parameter α, we can characterize the random walk as persistent for α > 0 and anti-persistent to α < 0.
The second moment of the position is given by
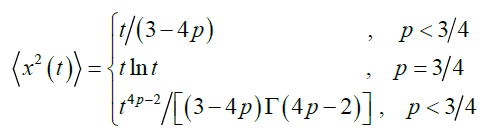 (4)
(4)
The diffusive behavior changes with the probability values p. For example, when p<3/4, the second moment is linearly dependent on t and the diffusion is regular (H=1/2). For p>3/4, the diffusion is characterized as superdiffusive and for the intermediate case, i.e., p=3/4, the second moment is described by a logarithmic function [5].
Additional information about the ERW model, such as probability distribution, the study of its limits, etc., can be verified in [5,14,15].
The Model
Our model consists of a pair of random walkers. Recently, two random walks were analyzed in which a walker makes a decision at instant t independently of the second. The first random walker represents an independent stochastic process (ERW model), while the latter makes decisions based on the history of the first (or its own history) with probability f (1 − f) [16]. In this way, the unilateral influence of the first walker on the second is evident. However, the first walker is not influenced by the second. The first walker is called “Professor” and the second “Student”. When f=0, the Student does not learn from the Professor and only makes decisions based on his/her own history, representing the maximum of restricted interests (it is associated with severe autism). As f grows, the interests of the student become less restricted and they learn from the Professor, and the maximum (minimum) learning occurs when f=1 (f=0). At the outset of microscopic dynamics, Student imitates (“learns”) the Professor’s decisions with probability f, but the Professor does not learn from the Student, i.e., the Student’s decisions are entirely unknown to the Professor so that the first random walker is not influenced by the decisions of the second one. If we consider that in neurological exams in children the analysis of communication and social interaction in multiple contexts are part of the routine, including repetitive patterns of behavior, the (medical) examiner will have knowledge of the patient’s actions and therefore, in the context of our problem, the Professor has knowledge of the Student’s actions, but is not influenced by these actions. Therefore, this problem leads us to the following question: how can the first random walker influence the second one and not be influenced by him? In other words, how can the Professor teach and not learn from the Student’s actions? But, if both can teach and learn, how can we call a process of Professor and Student? To solve this problem, however, we define that the interaction is bilateral, and the probability of the Professor of learning (not learn) from Student’s actions, is given by fP (1 − fP). Similarly, the probability of the student being able to learn (not learn) with the Professor is given by fA (1 − fA). In this way, as the two random walkers can learn from each other, both can learn Professor and Student labels. For reasons of order, we will call the ERW model Professor and the other one Student.
Our model describes the interaction between the two discrete random walkers (Professor and Student). We define the Professor as the ERW model, whose microscopic dynamics has already been described previously. The Student initiates his/her movement at the position Y0, at time t0=0 at every instant of time, the walker walks one step to the right or one step to the left, with probability p and (1 − p), respectively. The stochastic equation that quantifies Student’s steps is given by
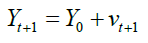 (5)
(5)
and νt+1 a random variable that assumes the values of σÃâ¦ÃÂ¥ when the random walker behaves just like the ERW model. The Student accepts the decisions of the ERW model with probability fA and rejects decisions with a complementary probability (1 − fA), when the walker makes decisions based on his or her own history. The memory is formed by a set of random variables νÃâ¦ÃÂ¥, Ãâ¦ÃÂ¥ < t, which the walker remembers as follows:
(a) in time t + 1 a number Ãâ¦ÃÂ¥ of the set {1, 2, ..., t} is chosen in an equiprobable way 1/t;
(b) the variable νt+1 is determined stochastically as: νt+1=νÃâ¦ÃÂ¥
In the first step, in the instant t=1, the walker is in position Y0, accepting (rejecting) the ERW model with probability fA (1 − fA), for this process, the stochastic evolution equation is given by
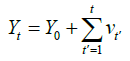 (6)
(6)
for all time. As the student accepts (rejects) Professor’s decisions with probability fA (1 − fA), we note that the random variable νÃâ¦ÃÂ¥ can be rewritten as
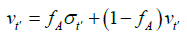 (7)
(7)
and thus, we rewrite the Student’s stochastic equation as
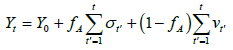 (8)
(8)
For the maximum non-learning limit, fA=0, Student recalls actions solely from its history and its stochastic equation is given by (6), at the other extreme, fA=1, when there is maximum interaction, the stochastic equation is written as
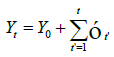 (9)
(9)
Therefore, with the exception of the first step Yz, the process is described by the ERW model.
Similarly, for the Professor, to encompass the ability to learn, making him susceptible to the actions of the Student, the dynamics of the Professor, will also be influenced by Student’s decisions with probability fP and not influenced with probability 1 − fP. The stochastic equation (2) is modified by the following transformation
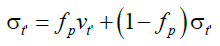 (10)
(10)
resulting in stochastic equation
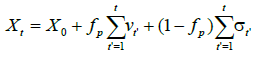 (11)
(11)
which describes the learning of the ERW model with respect to the Student. When fP=0, which quantifies the minimum of learning, the random walker behaves like the ERW model, while fP=1, quantifies the maximum amount of Professor learning in relation to student actions. For the maximum interaction, fP=1, the stochastic equation takes the following form:
 (12)
(12)
and νÃâ¦ÃÂ¥ the stochastic variable that represents the microscopic decisions in Student.
We can consider two cases for the probabilities of interaction between random walkers. The first case is when the likelihood of learning of the two hikers is equal, i.e., fP=fA and the second when fP ≠ fA. We address in this work the case where fP=fA and formulate our model under these conditions. The maximum (minimum) of perseverance that each (Professor or Student) will have in their actions, will occur for the quantitative probability values fP=fA=0 (fP=fA=1) which correspond to the minimum (maximum) of learning, respectively. Therefore, we can vary a single probability value by calling fP=fA=f and rewriting the equations (8) and (11) respectively as
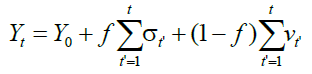 (13)
(13)
and
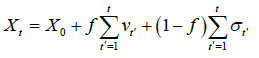 (14)
(14)
For the case of minimal learning, f=0, the models recover their ordinary results without mutual learning, with the stochastic equations (6) and (2) for the Student and for the ERW model, respectively.
Results
Based on the ERW model, we introduced a model of discrete random walks, which interact and express different diffusion regimes according to the variation of the parameter f. A regular parameter for making measurements of the different diffusion regimes in random walks is the Hurst exponent (H), present in the variance 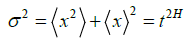 , which tends to spread in a non-linear fashion over time, to values of H≠1/2. For H<1/2 (H>1/2) the regime is termed subdiffusive (superdiffusive). For cases where the second moment of the position grows faster than the first, the following approximation can be used
, which tends to spread in a non-linear fashion over time, to values of H≠1/2. For H<1/2 (H>1/2) the regime is termed subdiffusive (superdiffusive). For cases where the second moment of the position grows faster than the first, the following approximation can be used 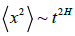 . The estimated means for our finite-length hikes are: 104 pairs of walks of size 107. The measurements of the Hurst exponent are estimated by the approximations
. The estimated means for our finite-length hikes are: 104 pairs of walks of size 107. The measurements of the Hurst exponent are estimated by the approximations 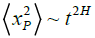 and
and 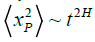 for the Student and Professor, respectively.
for the Student and Professor, respectively.
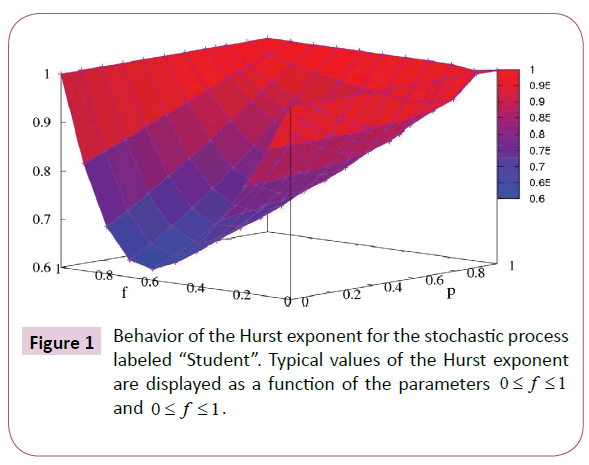
In Figure 1 typical measures of Student Hurst exponent are displayed. The measurements of H are presented according to the parameters 0 ≤ p ≤ 1 and 0 ≤ f ≤ 1, where f is the Student’s probability to imitate the Professor’s actions (ERW model), measures the different degrees of restriction of interest, with impact on Student’s diffusive regimes, as measured by the Hurst exponent. The restriction (non-restriction) interest end is quantified by f=0 (f=1), which is also the minimum (maximum) of inter- action. At point f=0, of maximum restriction of interests (higher degree of autism), the Student presents persistent microscopic behavior, characterized by measurements typical of the Hurst exponent H=1, which qualify the diffusive regime as ballistic. At the other extreme f=1, the point of least restriction of interests (lower degree of autism), surprisingly, we observe that, our model of mutual learning, presents H=1 in ballistic regime at the maximum of learning. For the interval 0<f<1, the Student’s diffusive regimes are integrally superdiffusive (H>1/2). For finitesize random walks, we obtain that the smallest measure of the Hurst exponent (H ∼ 0.62318), to f=0.6 and p=0.0.
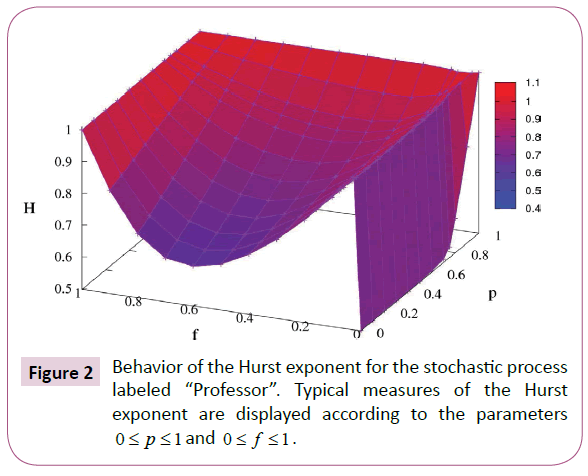
In Figure 2 typical measures of Professor Hurst exponent are displayed. Measurements of the exponent H are presented according to the parameters 0 ≤ p ≤ 1 and 0 ≤ f ≤ 1. In this case, f, the probability of the Professor Imitating Student actions implies that Student’s microscopic dynamics will influence the Professor’s microscopic dynamics, thus having an impact on the diffusive regimes of the ERW model. In the cases bordering on our model, when f=0, there is no learning, implying, therefore, that the measures of H exhibit the quantitative values of the ERW model, showing that at this limit, this does not depend on the microscopic decisions of the other random walker. At the extreme of maximum interaction, f=1, the Professor displays diffusive ballistic regime with values characterized by H=1. In the interval 0<f<1, for intermediate values of interaction, we obtain measurements of the Hurst exponent that characterize the superdiffusive regime (H>1/2), including the value of p=1/2 which is commonly known as a point characterized by having typical values of H=1/2 for discrete random walks, which have the characteristic of recording the decision made at every instant of time t, as can be seen in [6-13]. Except for f=0, when there is no learning, and the measures of H are representative of the overdiffusive regime, for the interval of 0 ≤ f ≤ 1. In the intervals of 0 ≤ p ≤ 1 and 0 ≤ f ≤ 1, there is an abrupt growth of the diffusion diagram, Figure 2 in the values of the Hurst exponent, where 0<f<0.1 we obtain H>1/2.
Conclusion
Autism spectrum disorders have inspired us to construct discrete random walks to assess Autism. We used two random walkers to study Autism. Based on the symptoms of pervasive developmental disorders (PDDs) and using the ERW approach, for a set of discrete random walk pairs, we studied how PDDs symptoms can affect diffusive walker regimes. The first random walker, called Professor, can learn from the second random walker, called Student, with probability fP. Similarly, the probability of the student being able to learn (not learn) with the Professor is given by fA (1 − fA). For simplicity, we consider the case where fP=fA=f, which we control in a unique way using the parameter f. Therefore, the Student can learn from the Professor and also, the Professor can learn from the Student with probability f, such that the microscopic decisions of both have an impact on the diffusive regimes of one another. The results are summarized in a way that addresses the changes in the diffusive regimes of the two random walkers.
The transitions in the Professor and Student diffusive regimes are summarized and presented below.
1. To the Professor:
(a) the Professor has the maximum of restricted interests, to f=0. At this limit, the diffusive regimes typical of the ERW model are recovered;
(b) we find an abrupt transition in the diffusive regime of the Professor, for the interval 0<f<0.1. This fact is characterized by the actions of the Professor, also being influenced by the student’s actions, having an impact on the diffusion regime of the ERW model;
(c) the diffusion regime for the Professor is characterized by measures of the exponent of Hurst H>1/2, for all p, except at point f=0, when the ERW models are recovered.
2. For the Student:
(d) we find a ballistic regime at the extremes f=0 and f=1. In these cases, the Student exhibits the maximum of restricted interests, the Professor’s actions do not influence their decisions and the dynamics are essentially deterministic. For f=0, there is no learning, so the Student presents the maximum restriction of interests. This characteristic may be associated with the repetitive behavior presented in the PDDs symptom listing, characterizing severe autism. In the extreme, f=1, there is the minimum of restriction of interests among random walkers, i.e., the Professor and the Student learn with the greatest probability. The parameter f quantifies how much, the Student and the Professor will present restricted interests, therefore for f=1, the Professor (Student) learns from the Student (Professor) with the maximum probability. Soon the Professor’s microscopic dynamics influence the dynamics as much as the Student’s microscopic decisions alter that of the Professor;
(e) we find an overdiffusive regime, for f>0. In this case, the random walker (Student) undergoes a diffusion transition from the ballistic regime to the superdiffusive regime. The parameter f quantifies how much, the Student and the Professor will present restricted interests, therefore for f=1, the Professor (Student) learns from the Student (Professor) with the maximum probability. in the region of mutual learning with maximum probability, results in a diffusive ballistic regime;
(f) we find a second transition in the diffusion regime, to f → 1, the Student undergoes a transition from the superdiffusive regime to the ballistic regime. At this limit, there is learning and the reduction of restriction of interests occurs, but restricted interests prevail in the region of maximum learning.
When the Professor and Student have restricted interests with probability f, the former behaves like the ERW model and the second shows ballistic behavior at point f=0. For f >0, random walkers exhibit the same diffusive behavior, characterized by the same quantitative values of the Hurst exponent. The minimum of restricted interests associated with DID symptoms are those in which they exhibit lower Hurst exponent values (occurs in finite-length walks for f ≈ 0.6), the larger the severity of the autistic degree (for f=0 and f=1).
References
- American Psychiatric Association (2013) Diagnostic and statistical manual of mental disorders: DSM5 (5th Edn).
- Paraan FNC, Esguerra JP (2006) Exact moments in a continuous time random walk with complete memory of its history. Phys Rev E 74: 032101.
- Peng CK, Buldyrev SV, Goldberger AL, Havlin S, Sciortino F, et al. (1992) Long-range correlations in nucleotide sequences. Nature 356: 168-170.
- Tavaré S, Giddings BW (1989) Mathematical methods for DNA sequences (Waterman MS Edn). CRC Press, Boca Raton, pp: 117-132.
- Schütz GM, Trimper S (2004) Elephants can always remember: exact long-range memory effects in a non-Markovian random walk. Phys Rev E 70: 045101.
- Cressoni JC, da Silva MAA, Viswanathan GM (2007) Amnestically induced persistence in random walks. Phys Rev Lett 98: 070603.
- Felisberto ML, Passos FS, Ferreira AS, da Silva MAA, Cressoni JC, et al. (2009) Sudden onset of log-periodicity and superdiffusion in non-Markovian random walks with amnestically induced persistence: exact results. Eur Phys J B 72: 427.
- da Silva MAA, Viswanathan GM, Ferreira AS, Cressoni JC (2008) Spontaneous symmetry breaking in amnestically induced persistence. Phys Rev E Stat Nonlin Soft Matter Phys 77: 040101R.
- Cressoni JC, Viswanathan GM, Ferreira AS, da Silva MAA (2012) Alzheimer random walk model: two previously overlooked diffusion regimes. Phys Rev E Stat Nonlin Soft Matter Phys 86: 042101.
- Borges GM, Ferreira AS, da Silva MAA, Cressoni JC, Viswanathan GM, et al. (2012) Superdiffusion in a non-Markovian random walk model with a Gaussian memory profile, Eur Phys J B 85: 310.
- Alves GA, de Araújo JM, Cressoni JC, da Silva LR, da Silva MAA, et al. (2014) Superdiffusion driven by exponentially decaying memory. J Stat Mech Theory Exp 2014: P04026.
- Moura TRS, Viswanathan GM, da Silva MAA, Cressoni JC, da Silva LR (2016) Transient superdiffusion in random walks with a q-exponentially decaying memory profile. Physica A: Stat Mech Appl 453: 259-263.
- Diniz RMB, Cressoni JC, da Silva MAA, Mariz AM, de Araújo JM (2017) Narrow log-periodic modulations in non-Markovian in random walks. Phy Rev E Stat Nonlin Soft Matter Phys 96: 062143.
- Baur E, Bertoin J (2016) Elephant random walks and their connection to Pólya-type urns. Phys Rev E Stat Nonlin Soft Matter Phys 94: 052134.
- da Silva MAA, Cressoni JC, Schütz GM, Viswanathan GM, Trimper S (2013) Non-Gaussian propagator for elephant random walks. Phys Rev E Stat Nonlin Soft Matter Phys 88: 022115.
- Moura TRS, Fulco UL, Albuquerque EL (2018) A random walk model to evaluate autism. Physica A: Stat Mech Appl 492: 1694-1699.
- Hurst HE, Black RP, Simaika YM (1965) Long-term storage: an experimental study. Constable, London, p: 145.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences